分類_Classification (Vol.14)

2018.04.25 株式会社システムインテグレータ

はじめに

前回は教師あり学習の中から回帰に使うアルゴリズムをいくつか解説しました。今回は、教師あり学習の分類の中から、ロジスティック回帰とk近傍法について説明します。ニューラルネットワークを学ぶつもりなのに、機械学習のアルゴリズムで足止めしているようで心苦しいのですが、ディープラーニングをやっていく上でも、基本的なアルゴリズムは理解しておいた方がいいので辛抱してお付き合いください。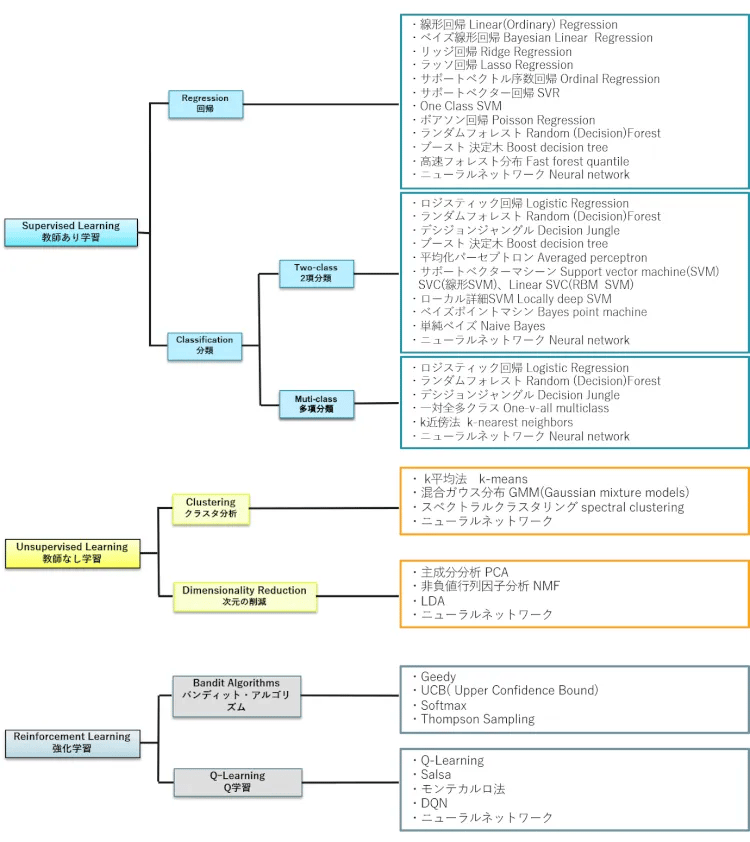

3つの機械学習法と統計的手法（再掲）

図1：3つの機械学習法と統計的手法（再掲）

分類(Classification)

分類には、2項分類(Two-class Classification）と多項分類(Multi-class Classification）があります。2項分類は、その名の通り2つに分類するものです。例えば製品検査で正常と異常に分けるのは代表的な2項分類です。一方、多項分類は3つ以上に分類するもので、例えば当社がホームページで無料公開している「花の名前を教えてくれるAI（AISIA FlowerName）」は、257種類の花を学習しているので、未知の花の写真を見てその中のどれかに分類してくれます。

(1)ロジスティック回帰

前回、回帰（Regression）のアルゴリズムの多くが分類(Classification)でも使われると説明しました。ロジスティック回帰もその1つで、”回帰”という名前がついていますが、実は”分類”でよく利用されます。

このお客は買うか買わないか、この患者は癌を発症するかしないか、このメールは迷惑メールか、こういうお客様たちはダイレクトメールに反応するか、などデータをもとにYes/Noに分類するのが2項分類です。Vol.11でやった「IT業界にB型が多い」という仮説が正しいかどうかも2項分類と言えます。

ロジスティック回帰は、一言で言うと”発生確率を予測して、確率に応じてYes/Noに分類するもの”です。う～ん、これだけだとまだ理解できないので具体例で説明しましょう。

あなたはストーカーです（おいおい、どんな例えだよ！）。近くに住む麻里ちゃんの通勤姿を一目でも見ることができれば幸せな一日です。朝はいいんです。毎朝、7時30分頃に自販機の影で待っていれば、ほぼ確実に見ることができます。問題は帰りです。そのまま帰宅するときは19時くらいに待っていればいいのですが、食事会などで遅くなる日があるので待ちぼうけの時もあります。

そこで、朝の服装を見て「今日は定時でそのまま帰宅するか」を予測をすることにしました。これまでの感覚では、定時で帰るかどうかは、その日の服装と曜日が因子要因になりそうです。そこで、その2つに着目して３か月のデータを取ってみました（表1）。

日	曜日	おしゃれ度	定時で帰宅
1日	月	おしゃれ	〇
2日	火	普通	〇
3日	水	普通	〇
4日	木	おしゃれ	×
5日	金	普通	〇
～
30日	木	普通	〇
31日	金	おしゃれ	×

表1：定時で帰ったかどうかの記録

[RELATED_POSTS]

3か月のデータを見る限り、どうも木曜日か金曜日におしゃれして出勤した場合は、遅く帰宅するようです。この法則をロジスティック回帰で見つけてみましょう。ただし、ここでは数式で説明しません。こんな感じで分類するのだというイメージがわかれば十分とします。

数式は使いませんが、せっかくなので難しい言葉を1つ覚えておきましょう。それは尤度です。え、読めない？ですよねぇ～。これは”ゆうど”と読みます。尤という字は、訓読みだと尤も（もっとも）で英語だとLikelihoodです。尤度は確率で表され、それを尤度関数と言います。そうです、Vol.11で登場した正規分布は確率分布なので尤度関数の1つです（図2）。

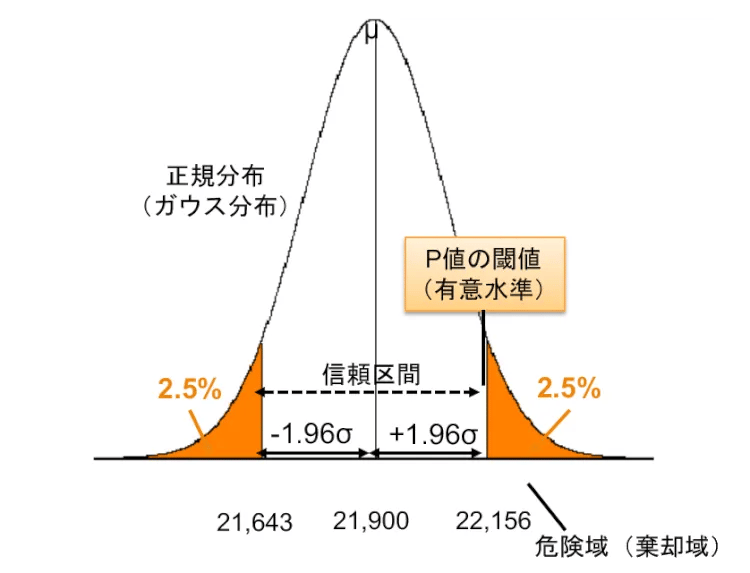
正規分布とP値（再掲）

図2：正規分布とP値（再掲）

もう1つ、関数が出たついでにロジスティック関数（≒シグモイド関数）も覚えておきましょう。これは、図3のようなS字の関数です。ポイントは、Y軸が0から1の範囲ということで、ある事象に応じた確率を尤度関数で求め、それを0～1の範囲で表すものです。上記の例では、2つの変数「曜日」と「おしゃれ」の組み合わせでxの値が決まり、それに応じた定時で帰る確率yが導き出されることになります。閾値（この図では真ん中の線）より右（ピンク）なら”定時で帰る”、左（ブルー）なら”遅くなる”という予測が立てられるわけです。

まあ、非常に大雑把な説明ですが、ここまで理解した上でもう1度、”発生確率を予測して、確率に応じてYes/Noに分類するもの”という定義を読めば、今度はわかった感じになると思います。

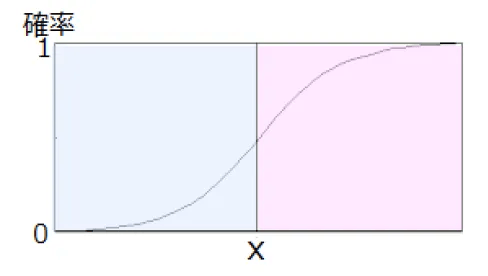
ロジスティック関数

図3：ロジスティック関数

(2)k近傍法

次は、多項分類のアルゴリズムをピックアップしましょう。k近傍法です。え、読めるけど自信がない？大丈夫です。合っていますよ。傍は傍観者の傍で、きんぼうほうと読みます。英語だとNearest Neighborで、直訳すると”最も近い隣人”ですね。k近傍法を一言で言うと、”類は友を呼ぶ”です。え、デフォルメし過ぎ？ですね。では、もう少し丁寧に言いなおすと、”ある未知の値を最も近いグループの仲間とする分類法”です。

前回、サポートベクターマシーン(SVM）の説明で使った職掌による性格分布を使って説明しましょう。図4は営業部門の人（青）と管理部門の人（緑）の性格分布です。SVMでは、この両者の間を最も川幅（マージン）が大きくなるように斜めに川を流して分類したんでしたね。

k近傍法

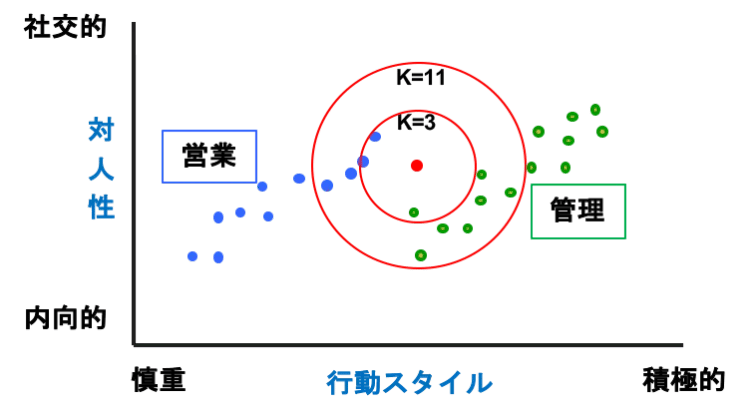
図4：k近傍法

今度はk近傍法で分類してみましょう。新しく入った人の性格診断を行ったところ、赤いドットのような結果になりました。さて、この人の適性は営業なのでしょうか、管理部なのでしょうか。

まずは、k（サンプル数）が3の例でやってみましょう。赤（未知のデータ）を中心に3個のサンプルが入る範囲で同心円を描くと、その中に青が2人、緑が1人が入ります。k近傍法は多数決で決めます。その範囲にデータが多い方の仲間とする分類法なので、この場合、新人は青の営業向きと判断されます。

k=11の例ではどうでしょうか。今度は、青4人、緑7人と緑が優勢となりますので、新人君は管理部向きということになります。近傍法は、こんな感じで、近い方の仲間に分類するというシンプルなアルゴリズムです。データ全体でなく近いデータだけで推測できるので、使いやすい方法です。なお、この例は2次元なので円で範囲を指定していますが、1次元なら線で、3次元なら球で近傍度合いを比較します（あまり高次なものには向かないとされています）。

上記のようにkの値により結果が異なるケースもあるので、kの値を決め方が重要ですね。よく使われているのは、総数の平方根をkとする方法です。今回はデータ総数が25なので、k=5あたりがよさそうということになるのですが、いくつかkを変えてよさそうなところを使ってみるのもいいでしょう。

k近傍法は、同じような嗜好を持つユーザーに分類する顧客セグメンテーションやレコメンデーションなどにもよく使われます。次回、解説するクラスタリングと同じ領域で使われますが、k近傍法は教師あり学習、クラスタリングは教師なし学習という違いがあることを覚えておいてください。